 GraphWiz:
GraphWiz:
Large language models (LLMs) have achieved impressive success across several fields, but their proficiency in understanding and resolving complex graph problems is less explored. To bridge this gap, we introduce GraphInstruct, a novel and comprehensive instruction-tuning dataset designed to equip language models with the ability to tackle a broad spectrum of graph problems using explicit reasoning paths. Utilizing GraphInstruct, we build GraphWiz, an open-source language model capable of resolving various graph problem types while generating clear reasoning processes. To enhance the model's capability and reliability, we incorporate the Direct Preference Optimization (DPO) framework into the graph problem-solving context. The enhanced model, GraphWiz-DPO, achieves an average accuracy of 65% across nine tasks with different complexity levels, surpassing GPT-4 which has an average accuracy of 43.8%. Moreover, our research delves into the delicate balance between training data volume and model performance, highlighting the potential for overfitting with increased data. We also explore the transferability of the model's reasoning ability across different graph tasks, indicating the model's adaptability and practical application potential. Our investigation offers a new blueprint and valuable insights for developing LLMs specialized in graph reasoning and problem-solving.

Figure 1: An example of solving the Connectivity task explicitly within natural language via LLMs.
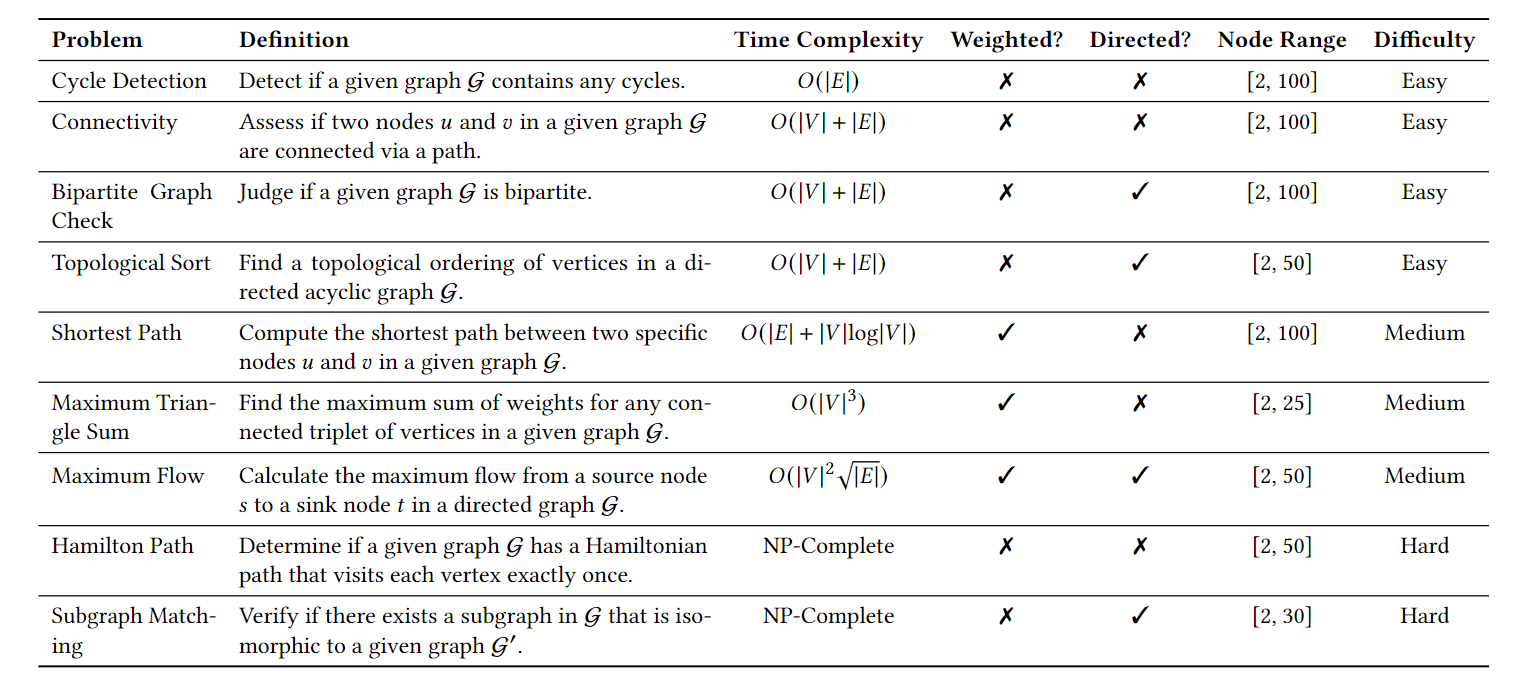
Table 1: Overview of nine tasks in GraphWiz with problem definition, time complexity, graph type (weighted/directed), node size range, and task difficulty. |V| and |E| indicate the number of nodes and edges in the graph.
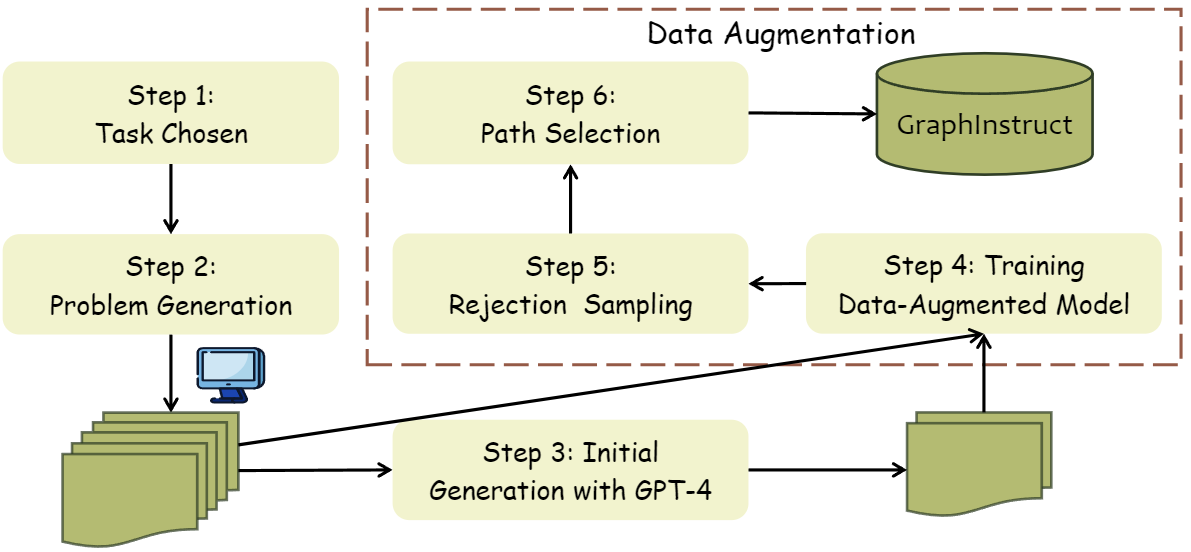
Figure 2: The overview of GraphInstruct collection process.
Based on the GraphInstruct dataset, we build GraphWiz, which is developed to optimize current LLMs' capabilities in solving graph problems with explicit reasoning paths. Our training methodology for GraphWiz is a novel two-phase process that first hones the model's ability to interpret and solve a wide range of graph problems using Mixed-Task Instruction Tuning. The subsequent phase, DPO Alignment, further sharpens the model's reasoning by training it to distinguish between more and less effective problem-solving paths. This innovative approach, particularly the use of DPO in the realm of graph problems, represents a pioneering step in teaching LLMs not just to output explicit answers, but to develop and follow a logical reasoning process that mimics expert problem-solving behavior.
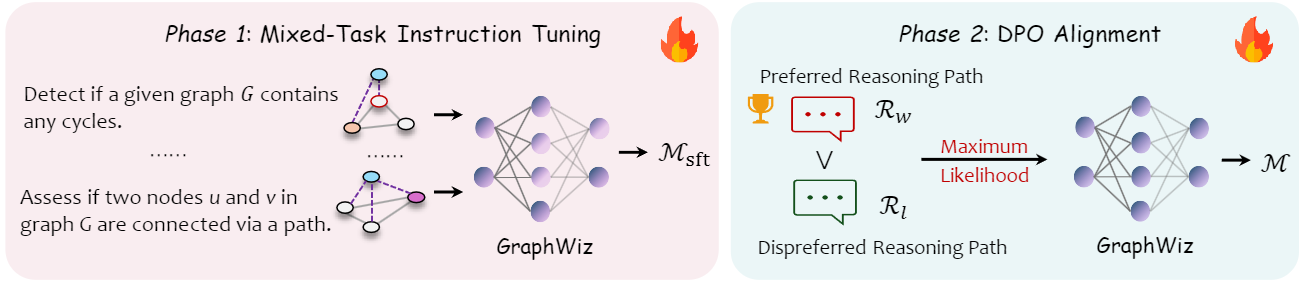
Figure 3: Training pipelines of GraphWiz.

Figure 4: A typical case of GraphWiz and GPT-4.
In this component, we present a case study of a complex cycle detection problem that involves an undirected graph with 89 nodes in Figure 4, a scale that poses substantial challenges even for human solvers. For a human to detect a cycle in such an extensive graph would require external aids or substantial time, as it is impractical to resolve purely through mental computation. We could observe that GPT-4 outputs a very short incorrect answer, which could arise from the model's constraints in processing long inputs or from an erroneous interpretation of the graph's intricate structure. This limitation reflects the challenges that conventional LLMs encounter when adapting to graph-theoretic problems. In contrast, GrphWiz correctly detects a cycle, providing a clear and detailed reasoning path. This demonstration of GrphWiz's spatial reasoning and memory retention capabilities is significant. It indicates that the model has effectively internalized the principles of graph theory to the extent that it can autonomously navigate through and reason about large-scale and complex graph structures. This case study is a testament to the feasibility of employing GraphWiz for sophisticated graph problems. The model's ability to accurately resolve such complex tasks suggests it has substantial practical applications, offering a robust tool for researchers and practitioners.
You may refer to related work that serves as foundations for our framework and code repository, such as NLGraph and GraphQA . We also partially draw inspirations from MathOctopus. For more details about Graph+LLM, you are welcome to follow our survey and repository.
@articles{chen2024graphwiz,
title={GraphWiz: An Instruction-Following Language Model for Graph Problems},
author={Nuo Chen, Yuhan Li, Jianheng Tang, Jia Li},
journal={arXiv preprint arXiv:2402.16029},
year={2024}
}